EL QUINTO ESTADO DE LA MATERIA.

CONDENSADO

DE

BOSE - EINSTEIN

En física, el condensado de Bose-Einstein es el estado de agregación de la materia que se da en ciertos materiales a muy bajas temperaturas. La propiedad que lo caracteriza es que una cantidad macroscópica de las partículas del material pasan al nivel de mínima energía, denominado estado fundamental. El condensado es una propiedad cuántica que no tiene análogo clásico.
Debido al Principio de exclusión de Pauli, sólo las partículas bosónicas pueden tener este estado de agregación. Esto quiere decir que los átomos se separan y forman iones. A la agrupación de partículas en ese nivel se le llama condensado de Bose-Einstein.

En la década de 1920, Satyendra Nath Bose y Albert Einstein publican conjuntamente un artículo científico acerca de los fotones de luz y sus propiedades. Bose describe ciertas reglas para determinar si dos fotones deberían considerarse idénticos o diferentes. Esta se llama la Estadística de Bose (o a veces la Estadística de Bose-Einstein), y Einstein aplica estas reglas a los átomos preguntándose cómo se comportarían los átomos de un gas si se les aplicasen estas reglas. Así descubre los efectos que vienen del hecho de que a muy bajas temperaturas la mayoría de los átomos están al mismo estado cuántico, que sería el menos energético posible.
Imagínese una taza de té caliente, las partículas que contiene circulan por toda la taza.

Sin embargo cuando se enfría y queda en reposo, las partículas tienden a ir en reposo hacia el fondo.
Análogamente, las partículas a temperatura ambiente se encuentran a muchos niveles diferentes de energía. Sin embargo, a muy bajas temperaturas, una gran proporción de éstas alcanza a la vez el nivel más bajo de energía, el estado fundamental.

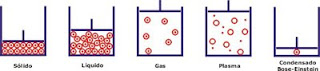
A la agrupación de partículas en ese nivel inferior se le llama Condensado de Bose-Einstein (BEC), porque la demostración está hecha de acuerdo con las ecuaciones de Einstein. Lo que seguramente no pudo imaginar es lo extraño que se vería una masa de materia con todos sus átomos en un solo nivel. Esto significa que todos los átomos son absolutamente iguales. No hay medida que pueda diferenciar uno de otro. Se trata de un estado de coherencia cuántica microscópico.

http://www.youtube.com/watch?v=EaVCIN2s6qo&feature=PlayList&p=1DF0376C559E046B&playnext=1&playnext_from=PL&index=21

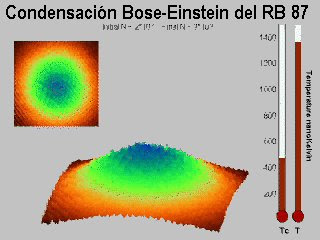
http://www.youtube.com/watch?v=6j1S7Sp-Ta4

La estadística de Bose-Einstein es un tipo de mecánica estadística aplicable a la determinación de las propiedades estadísticas de conjuntos grandes de partículas indistinguibles capaces de coexistir en el mismo estado cuántico (bosones) en equilibrio térmico. A bajas temperaturas los bosones tienden a tener un comportamiento cuántico similar que puede llegar a ser idéntico a temperaturas cercanas al cero absoluto en un estado de la materia conocido como condensado de Bose-Einstein y producido por primera vez en laboratorio en el año 1995. El condensador Bose-Einstein funciona a temperaturas cercanas al cero absoluto, -273,16°C(0 Kelvin). La estadística de Bose-Einstein fue introducida para estudiar las propiedades estadísticas de los fotones en 1920 por el físico hindú Satyendra Nath Bose y generalizada para átomos y otros bosones por Albert Einstein en 1924. Este tipo de estadística está íntimamente relacionada con la estadística de Maxwell-Boltzmann (derivada inicialmente para gases) y a las estadísticas de Fermi-Dirac (aplicables a partículas denominadas fermiones sobre las que rige el principio de exclusión de Pauli que impide que dos fermiones compartan el mismo estado cuántico).
La estadística de Bose-Einstein se reduce a la estadística de Maxwell-Boltzmann para energías suficientemente elevadas.

Formulación matemática
El número esperado de partículas en un estado de energía i es:
donde:

http://www.flickr.com/photos/rodolfoandradegarcia/

http://www.slideshare.net/RODOLFOANDRADEGARCIA